Can you make your problem linear?

We want our problem to solve to be in the form

$$d = Gm$$

However, some problems won't be linearly separable like this and will take some re-arranging to get into this form. Even then, we simply won't be able to put some problems into this form. In this section we'll look at an example of a problem that initially doesn't fit into this form but can be linearized with a but of re-arranging.

An example of a non-linear problem that can be linearized

In this problem we will look at Moore's Law, which is a theory that states that the average number of transistors in integrated circuits doubles every 2 years (approximately). We will fit an exponential curve to data of the number of transistors in integrated circuits over the years to see if this rule holds. The form of the curve to fit a basic exponential of the form.

$$N = Ae^{Bt}$$

The first problem will come across is that this exponential equation doesn't easily fit into our $in d=Gm $in formula. But can we transform the equation somehow to fit into this formula?

Okay, enough teasing, if we take the natural log of both side of this equation then we can separate out the model variable into a simple multiplication of model variables and the environmental variables which will be used to form the forward operator, $in G $in

$$\ln{N} = \ln{A} + Bt$$

Now this new form of the equation is a simple straight line fit the model variables being to $in \ln{A} $in and $in b $in. From here we can use the same approach as in the linear least squares regression example but with an even simpler forward operator as we no longer need the quadratic term in in the $in X $in variable (which will be time in our example).

$$G= \begin{bmatrix} x_{1} & 1 \\ x_{2} & 1 \\ \vdots & \vdots\\ x_{Nd} & 1 \\ \end{bmatrix} $$

In terms of applying this in python, we follow the exact same logical as we used before with the exception that we now pre-process our data by taking the natural logarithm of the recorded data (number of transistors in this example) before sending the data into the functions that we made in the linear least squares topic.

First we'll read in the data from a CSV file, extract the data and take it's natural logarithm, and also extract the time samples

df = pd.read_csv('moores_law.csv', header=None)
transistors = np.log(df[0].values.T)
year = df[1].values.T

Note that we have taken the transpose of the data values, this is important as the inverse procedure involves multiplying matrices in which case the orientation of the data is important. For instance, if we want the matrix product $in G^{T}G $in to be square and of size $in N_{m} $in x $in N_{m} $in then the forward operator needs to be created such that each row corresponds to the environmental variables for each specific data example, i.e. in this example each row corresponds to the specific time instance of the recorded data. If the data was arranged differently then the calculation couldn't be done using the equation we have set out thus far. You could reformulate the equation for this new paradigm though.

polynomial_degree = 1
model = linearInversion(transistors, year, polynomial_degree, 0)
plotting(transistors, year, model, 'ln(transistors)','year', polynomial_degree)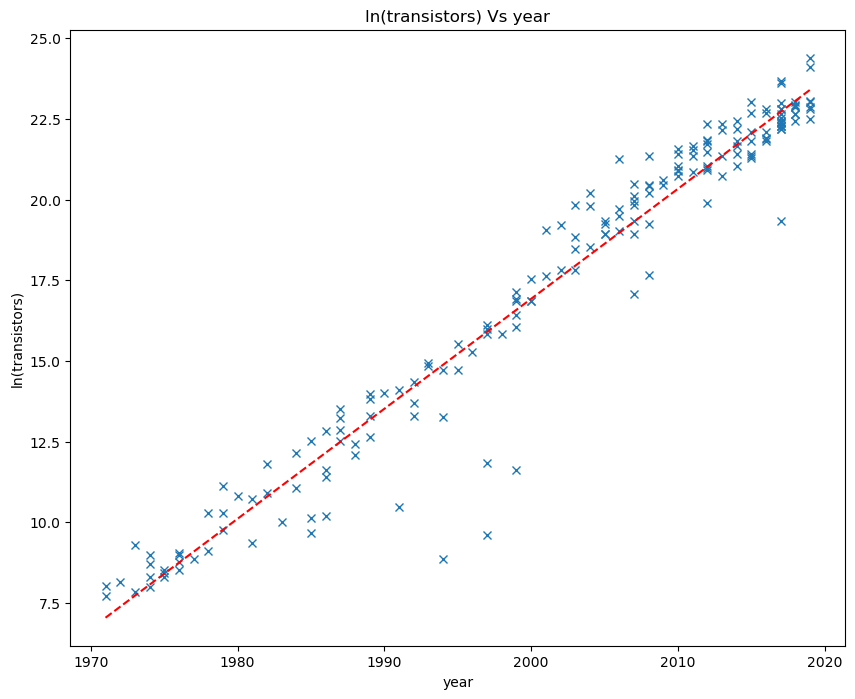

print(model)

[ 3.40910150e-01 -6.64891903e+02]

The model we have fit agrees remarkably well with Moore's law and shows that the average number of transistors in an integrated circuit is doubling every 2.03 years (to 2 decimal places). We come to this conclusion by noting that if the number of transistors were to double this would be equivalent to an ln(2) increase in the natural log of the number of transistors. Given the gradient above, how many years would it take to reach an increase of ln(2)? The answer would be ln(2) divided by the gradient, which is approximately 2.03.

The method used here to linearize our problem may not always work and it may not be possible to linearize our problem. In this case, what do we do? A common solution to this scenario is given in the next section where we will cover non-linear least squares inversion.

Non-linear least squares inversion